Normalverteilung • Definition, Berechnung und Beispiel · [mit Video]

Um für unser Beispiel die Standardabweichung zu berechnen, ziehen wir also einfach die Wurzel aus der Varianz: $\Large{\sigma = \sqrt[]{3,6} \approx 1,9}$ Was sagt uns die Standardabweichung? Die Standardabweichung gibt die Streuung der Einzeldaten um den Mittelwert an. Mit ihrer Hilfe können wir sagen, ob ein Durchschnittswert repräsentativ.
Die Varianz verstehen und berechnen + Varianz Rechner
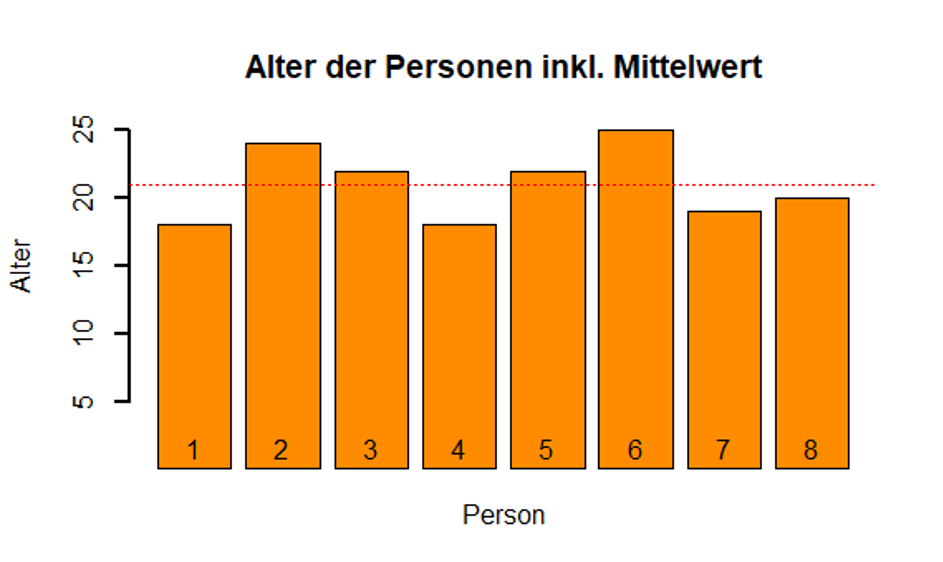
Die Varianz im Beispiel ist schwer interpretierbar: eine Varianz von 16 bei Daten, die nur von 1 bis 12 (Jahren) reichen. Aus der Varianz lässt sich aber einfach die aussagekräftigere Standardabweichung berechnen. Die Varianz hat zudem den Nachteil, dass sie empfindlich gegenüber Ausreißern ist (da die Abstände quadriert werden).
Varianz · einfache Erklärung, Definition (Stochastik) · [mit Video]

Die Varianz (von lateinisch variantia „Verschiedenheit" bzw. variare „ [ver]ändern, verschieden sein") ist ein Begriff der Wahrscheinlichkeitsrechnung. Sie ist ein Maß für die Streuung reeller Werte um einen Mittel-, bzw. Erwartungswert. (Die Streuung um einen Erwartungswert stellt dabei die allgemeinere Betrachtungsweise dar.
Varianz Beispiel Video YouTube

Varianz. Die Varianz ist ein Maß für die Abweichung einer Zufallsvariablen X X von ihrem Erwartungswert \mu μ in der Stochastik. Sie beschreibt die mittlere quadratische Abweichung der Werte der Zufallsvariablen zum Erwartungswert. Die Varianz einer Zufallsgröße ist eng mit ihrer Standardabweichung verknüpft.
Streuungsmaße Varianz, Standardabweichung und Variationskoeffizient YouTube

In dem Beispiel sehen wir, dass die Varianz aufgrund der Einheit (z.B. Jahre 2) nicht sehr aussagekräftig ist. Um eine Aussage über die Streuung machen zu können, müssen wir daher zunächst die Standardabweichung aus der Varianz berechnen. Merke Die Standardabweichung erhalten wir, indem wir die Wurzel aus der Varianz ziehen.
Varianz Formel / Grundlagen der Statistik Varianz und Standardabweichung Varianz ist das maß

Was sagt die Varianz aus Beispiel? Haben verschiedene Tiere ein Durchschnittsgewicht von 10 kg, gibt es darunter auch Tiere, deren Gewicht größer oder kleiner ist, als 10 kg. Bei einer großen Varianz haben viele Tiere ein anderes Gewicht als 10 kg und bei einer kleinen Varianz haben die meisten Tiere ein Gewicht von 10 kg.
Varianz Mathepedia
Wenn du aus deiner Stichprobe allerdings auf die Grundgesamtheit schließen möchtest, dann nutzt du in der Formel 1/(n-1) (man spricht dann von der Stichprobenvarianz). Zusammenfassung zum Thema Varianz und Standardabweichung: Die Varianz und die Standardabweichung sind die beiden wichtigsten Streuungsmaße der deskriptiven Statistik.
Wie wird die Varianz und die Standardabweichung allgemei... Analysis und Stochastik Repetico

Sie ist eigentlich nichts anderes als die Wurzel der Varianz. Um aus Jahre² also die normalen Jahre zu erhalten, ziehen wir die Wurzel:. Was sagt die Varianz aus Beispiel? Die Varianz zeigt an, wie sich die Beobachtungswerte um den Mittelwert bei einer Beobachtung herum verteilen. Sie gehört somit zu den Streuungsmaßen.
Varianz Und Standardabweichung Einer Stichprobe Berechnen

Im Unterschied zur Varianz, die die Variabilität der betrachteten Zufallsvariablen misst, ist die Kovarianz ein Maß für die gemeinsame Variabilität von zwei Zufallsvariablen. Aus dieser Definition der Kovarianz folgt, dass die Kovarianz einer Zufallsvariablen mit sich selbst gleich der Varianz dieser Zufallsvariablen ist.
Varianz Berechnen Excel Varianz und Standardabweichung berechnen CHIP Genau dies sehen

Varianz und Standardabweichung einfach erklärt. Die Varianz (Var) gibt dir an, wie sehr die Ergebnisse vom Erwartungswert abweichen. Ist die Varianz groß, so streuen die Werte eher stark um den Erwartungswert. Ist die Varianz gering, so streuen die Werte eher wenig um den Erwartungswert. Die Standardabweichung \sigma σ ist die Wurzel aus der.
Varianz Und Standardabweichung Einer Stichprobe Berechnen

Varianz Formel Die Formel zur Varianz schaut kompliziert aus, ist aber sehr einfach anzuwenden.. ist das Zeichen für die Varianz (bei Zufallsexperimenten); ist der Mittelwert, bzw.Erwartungswert; ist das Ergebnis des Zufallsexperiments; beschreibt, dass erst eine Summe der gewichteten quadratischen Abweichungen vom Mittelwert berechnet wird; steht für die Wahrscheinlichkeit eines Ereignisses .
Was ist die Varianz? Wie berechne ich die Standardabweichung? Streuungsmaß in der Statistik

Was sagt die Streuung in der Statistik aus? Die Streuung gibt an, wie weit die Werte. Die Varianz verstehen und berechnen + Varianz Rechner Die Varianz gibt an, wie sich deine Beobachtungswerte um den Mittelwert aller Beobachtungen verteilen. Lies nach, wie du sie berechnest. 181.
Rechnen mit Varianzen (Rechenregeln, Translationsinvarianz der Varianz) YouTube

Die Standardabweichung ist die Quadratwurzel aus der Varianz. Sie ist manchmal nützlicher, weil die Quadratwurzel die Einheiten aus der Analyse entfernt.. Wenn man zum Beispiel sagt, dass eine Erhöhung von X um eine Einheit Y um zwei Standardabweichungen erhöht, kann man die Beziehung zwischen X und Y unabhängig von den Einheiten, in.
Varianz berechnen mit absoluten Häufigkeiten YouTube

Die Standardabweichung ist die Wurzel aus der Varianz und somit quasi ihre "Tochter". Beide beschreiben bzw. quantifizieren die Streuung der Werte um den Mittelwert eines Datensatzes herum, geben also Auskunft darüber, wie sehr sich die Versuchspersonen im betreffenden Merkmal unterscheiden. Sie können nur bei metrischen Daten angewendet.
c) Die graphische Darstellung der Varianzkomponenten

Was sagt die Varianz in Statistik aus? In der Statistik gibt es verschiedene Messgrößen, die dazu dienen, eine Verteilung einer Zufallsvariable zu charakterisieren. Eine davon ist die Varianz. Die Varianz einer Zufallsvariable gibt den Umfang der Streuung der Werte der Variable an. Die Varianz wird in der Regel als eine quantitative Maßzahl.
Konfidenzintervall für Erwartungswert, Varianz und Median Statistik Wiki Ratgeber Lexikon

Nachteil der Varianz ist, dass sie aufgrund der Quadrierung eine andere Einheit als die beobachteten Messwerte besitzt. Auf den ersten Blick können somit keine konkreten Aussagen über die Streuungsbreite abgeleitet werden. In der Praxis wird daher häufig die Standardabweichung, die sich aus Quadratwurzel der Varianz ergibt, herangezogen.